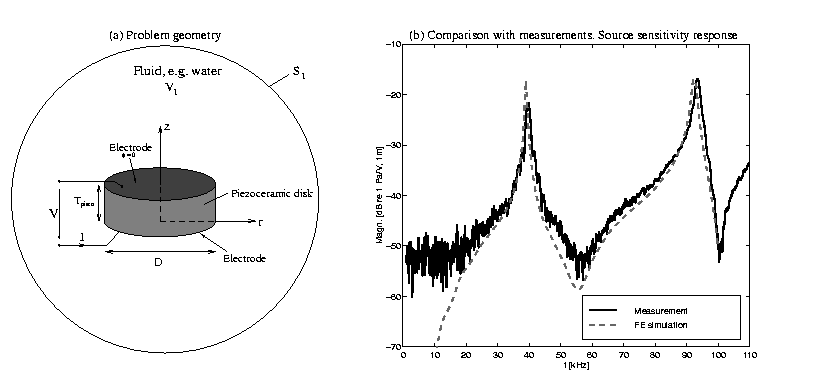
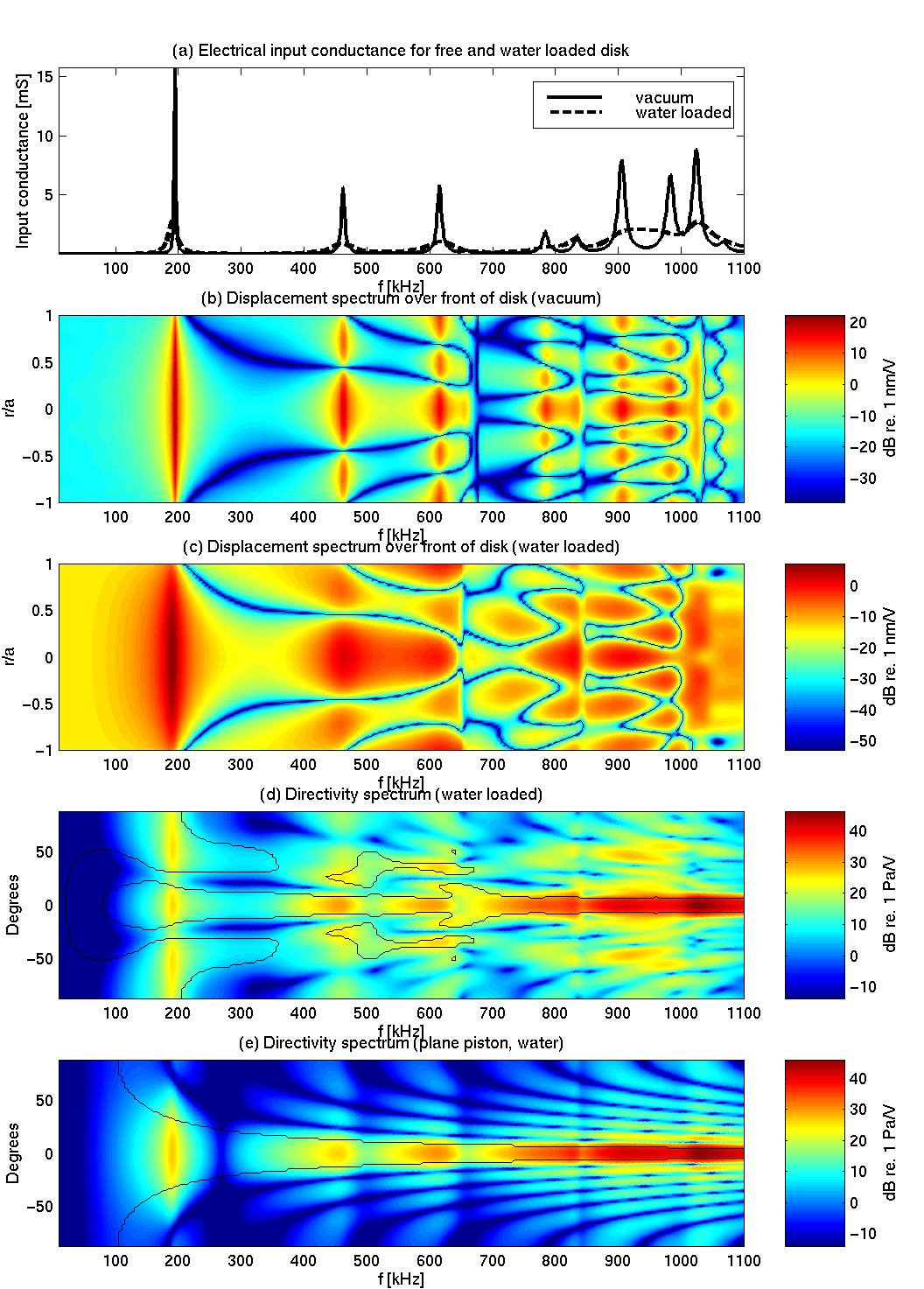
Finite Element Modeling of Piezoceramic Disks including Radiation into a Fluid Medium Jan Kocbach1, Per Lunde2 and Magne Vestrheim1 1University of Bergen, Department of Physics, Allégt. 55, N-5007 Bergen, Norway 2Christian Michelsen Research AS, P.O. Box 6301, N-5892 Bergen, Norway Introduction Finite element (FE) modeling is a valuable tool for transducer construction, and may be both time- and cost-saving in practical design. This has been the longterm motivation for the development of a FE program for axisymmetric piezoelectric transducer structures including radiation into a fluid medium at UoB and CMR. Results for piezoceramic disks [1,2,3] and for piezoceramic disks with a front layer of varying thickness [4,5], where the effect of fluid loading has been neglected, have been presented in previous works. In the present work, the effect of the surrounding fluid medium is included in the FE formulation, using fluid finite elements and infinite wave envelope elements of variable order [6,7]. Using this FE formulation, the effect of fluid loading on a piezoceramic disk has been investigated, and the vibration on the front face of the piezoceramic disk has been compared to the resulting radiated sound pressure field, and to the corresponding sound pressure field radiated from a plane piston with the same radius. Method The FE formulation used for the analysis of axisymmetric piezoelectric transducer structures vibrating in vacuum has been described in detail in Ref. kocbach1999a. In the present paper, focus is set on the modeling of the sound pressure field radiated from the piezoceramic transducer structure into an infinite fluid medium. Consider a piezoelectric disk radiating into a fluid of infinite extent, as shown in Fig. 1(a). It is of interest to be able to calculate the near and far field sound pressure field radiated from the piezoelectric disk, the directivity pattern and the source sensitivity response for a large frequency band. The methods used for the modeling of the infinite fluid medium which are most often found in the literature, may be divided into two main categories: 1. The fluid medium is modeled using the Boundary Element (BE) method (see e.g. Refs. kirkup1998,schenck1967,amini1992,balabaev1996), where fluid boundary elements are coupled directly to the piezoelectric finite elements used for the modeling of the piezoelectric disk. When the BE method is used, it is only necessary to discretize the boundary of the piezoelectric disk. 2. Part of the fluid medium adjacent to the piezoelectric disk [the volume V1 in Fig. 1(a)] is modeled using fluid finite elements, and some mechanism is applied at the artificial boundary S1 to minimize the reflections from the artificial boundary. This mechanism may either be various types of dampers [12] (e.g. plane wave dampers), which absorb certain parts of the outgoing sound field, matching to analytical solutions [13], non-reflecting boundary conditions (e.g. the Dirichlet-to-Neumann global condition [14]), or infinite elements [6,7,15,16]. When the infinite element approach is used, the entire infinite fluid region outside the artificial boundary S1 is modeled using elements of infinite extent, where the infinite domain is mapped onto a finite domain using special mapping functions.     Figure 1: (a) Problem geometry. (b) Comparison between measured and simulated voltage source sensitivity response (Sv) for a PZT-5A disk in air.

The BE method seems attractive because there is no need to mesh the fluid region. However, due to evaluation of singular integrals, and the fact that the BE method is non-local, the calculation of the BE matrices is computationally intensive [10]. The BE matrices must be calculated at each frequency of interest, and it is computationally intensive to calculate the radiated sound pressure field for many points in the near and far field, because a matrix equation must be solved for each point where the radiated sound pressure field is sought [15]. Of the methods where part of the fluid medium is modeled using fluid finite elements, the infinite element approach is especially suited for the present work, because the sound pressure field in the near and far field is easily calculated for many points using simple interpolation and mapping functions, and the FE matrices must be set up only once, even if the solution is sought for a wide frequency band [7]. One drawback with this approach is that for high frequencies many fluid finite elements must be used to model the volume V1, resulting in large FE matrices. However, the FE matrices are sparse and banded, making the solution time comparable to the solution time for the much smaller dense FE/BE matrices [15]. In addition, the artificial boundary S1 may be set in the near field for some types of infinite elements, like e.g. the infinite wave envelope elements of variable order [6,7]. Some recent studies have shown that for large problems, the solution time is longer when boundary elements are used to model the fluid than when finite and infinite elements are used to model the fluid, when the analyses is made for more than a few frequencies [15,17,18]. In the present work, the infinite element approach is chosen for the modeling of the fluid region. There are several types of infinite elements available (see e.g. Refs. astley1998,cremers1994,burnett1994,bettes1992,shirron1995,gerdes1998), with varying properties. Here it is chosen to use the infinite wave envelope elements of variable order [6,7]. This choice is based on the good performance reported for these infinite elements [7], and the fact that these infinite elements may be applied in the near field[7]. Furthermore, the far field sound pressure field may be calculated easily when this infinite element formulation is used[7]. Verification The FE formulation has been implemented in the FE code FEMP, "Finite Element Modeling of Piezoelectric structures". The FE results for the piezoelectric finite elements in FEMP have been verified previously through comparison with other FE results (including the FE codes ANSYS, ABAQUS and CAPA), measurements and theory [1,2]. For example, less than 8 ppm deviation has been found between resonance frequencies calculated using FEMP and corresponding resonance frequencies calculated using ANSYS, ABAQUS and CAPA for piezoceramic disks with diameter over thickness ratio varying between 0.2 and 20 [1]. The implementation of the fluid finite and infinite elements has been tested through comparisons with the analytical on-axis solution [20] and the numerical integration of a transformed Kings integral for the sound pressure field radiated from a plane piston mounted in an infinite rigid baffle. In the comparisons, the distance at which the infinite elements are applied, the ka-value of the problem, and the number of elements per wavelength used in the fluid region have been varied. Here a is the radius of the piston and k is the wavenumber in the fluid. The ka-value has been varied between 0.1 and 30. Good quantitative agreement has been achieved when S>0.3 and more than 5 elements are used per wavelength, where S=z lambda/a^2, z is the axial distance, and lambda is the wavelength in the fluid medium. For example, when using 5 elements per wavelength for ka=30, the error relative to the maximum pressure value is below 2.5% in both the near field and far field. When using 5 elements per wavelength for ka=5, the corresponding maximum error is 0.5%, and when using 10 elements per wavelength for ka=5, the corresponding maximum error is 0.03%. The complete FE model including piezoelectric finite elements, fluid finite elements, fluid infinite elements and the coupling between piezoelectric and fluid finite elements has been tested through comparison with measurements for a PZT-5A (see Ref. pzt1976 for material properties) disk in air. The PZT-5A disk has diameter 50.06 mm and thickness 9.98 mm. In Fig. 1(b) the simulated voltage source sensitivity response (Sv) of the disk is compared to corresponding measurements, and good qualitative agreement is found. Analysis For the analysis, a PZT-5A [21] disk with diameter 10.0 mm and thickness 2.0 mm is chosen. About 5 quadratic elements are used per wavelength in both the piezoelectric disk and in the fluid region for the highest frequencies, and the infinite elements are applied at a distance of S=0.35 or larger. In Fig. 2(a) the electrical input conductance for the free disk and the water loaded disk is compared, to examine the effect of fluid loading. It is seen that when water loading is added the response is damped for all resonances, most peaks are broadened, and most resonance peaks are shifted either up or down in frequency. For example, the resonance peak for the first radial mode is shifted down from 195kHz to 190kHz due to the fluid loading, whereas the 3rd peak, which corresponds to the 3rd radial mode strongly coupled to the edge mode, is shifted to a higher frequency. Some vibrational modes, like the one just below 800 kHz, is not seen at all for the water loaded case, whereas it is seen clearly for the free disk case. In Fig. 2(b) the normal displacement over the front face of the disk is shown as a function of frequency (displacement spectrum), for the case where the disk is vibrating in vacuum. A corresponding displacement spectrum for the water loaded case is shown in Fig. 2(c), for comparison. Analogous to what is observed for the electrical input conductance, the resonances are broader for the water loaded case than for the free disk case. In the water loaded case, the whole front of the disk is vibrating in phase for most of the frequency band between 1000 kHz and 1100 kHz, whereas there is stronger coupling to the radial modes in this frequency band for the free disk case. Also, the fluid loading makes the edge mode less distinct. In Fig. 2(d) the sound pressure level at a distance of 1.0 m from the center of the front surface of the disk is shown as a function of angle and frequency (directivity spectrum) for the fluid loaded case. For frequencies around the first radial mode, sidelobes with sibelobelevel only a few dB below the level of the main lobe are seen at about 60 degrees. Analysis of the FE simulations of the sound pressure in the near field has shown that this is due to the strong interference between the sound pressure field radiated from the front and the circular edge of the disk (not shown here). The same effect, though weaker, is seen around the second radial mode, and to some extent around the third radial mode. At frequencies between about 1000 and 1080 kHz, the frequency band around the thickness extensional mode, there is a main lobe with a -6dB width of about 12 degrees, and with side lobe level of -20 dB. In Fig. 2(e) the corresponding directivity spectrum for a plane piston mounted in a rigid baffle calculated using the analytical far-field solution [20], is shown. The vibrational amplitude is set to the average displacement over the front of the piezoceramic disk at each frequency, and the radius of the plane piston is the same as the radius of the piezoceramic disk. When comparing Fig. 2(e) to the directivity spectrum for the piezoceramic disk shown in Fig. 2(d), it is seen that the directivity spectrum is similar for frequencies above 800 kHz, although the width of the main lobe is smaller, and the side lobe level is somewhat higher (-17.5 dB). The on-axis sound pressure level (source sensitivity response), is very similar for the two different calculations, especially at the resonance peaks.    Figure 2: (a) Electrical input conductance for a PZT-5A disk with D/T ratio equal to 5 with and without water loading. (b) The absolute value of the normal displacement at the front of the disk as a function of frequency using a dB scale, for the case where the disk is vibrating in vacuum. The zero-values of the displacement are shown using solid lines. (c) A corresponding displacement spectrum for the water loaded case. (d) Sound pressure level at a distance of 1.0 m from the center of the front surface of the disk is shown as a function of angle and frequency (directivity spectrum) for the fluid loaded case. Solid lines denote the -6 dB angle. (e) The corresponding directivity spectrum for a plane piston with an amplitude equal to the average displacement over the front of the piezoceramic disk at each frequency. The plane piston has the same radius as the piezoceramic disk, and is mounted in a rigid baffle.

Conclusions and further work A FE code for axisymmetric piezoceramic transducers including radiation into a fluid medium has been implemented. The infinite wave envelope elements of variable order have been chosen to represent the infinite fluid medium. The FE results have been compared to an analytical solution and measurements, with good quantitative and qualitative agreement, respectively. Also, the effect of fluid loading on a piezocermic disk has been investigated, and the displacement spectrum over the front of the disk has been compared to the directivity spectrum for the disk and the corresponding directivity spectrum for a plane piston with the same radius as the piezoelectric disk, mounted in an infinite rigid baffle. Acknowledgements The work described here has been supported by a grant from the Research Concil of Norway. The authors would also like to acknowledge T. M. Skar at the University of Bergen for providing measurements on a PZT-5A disk. Bibliography 1 J. Kocbach, P. Lunde, and M. Vestrheim, ``FEMP, Finite Element Modeling of Piezoelectric structures. Theory and Verification for piezoelectric disks,'' Scientific/Technical Report No. 1999-07, Department of Physics, University of Bergen, Norway, 1999. 2 J. Kocbach, P. Lunde, and M. Vestrheim, ``FEM-Analysis of piezoelectric disks - method and testing,'' in Proc. of 20th Scandinavian Symposium on Physical Acoustics, Ustaoset, Norway, edited by H. Hobæk (Department of Physics, University of Bergen, February 1997), pp. 60-61. 3 J. Kocbach, P. Lunde, and M. Vestrheim. ``Resonance frequency spectra with convergence tests of piezoceramic disks using the finite element method''. Submitted to the J. Acoust. Soc. Am.. 4 J. Kocbach, P. Lunde, and M. Vestrheim. ``FE simulations of piezoceramic disks with a front layer of varying thickness''. Presented at the IEEE Int. Ultrason. Symp., Nevada, October 1999. 5 J. Kocbach, P. Lunde, M. Vestrheim, and E. Bjørndal, ``Piezoelectric disks with a front layer. Comparisons of FEM with experimental data,'' in Proc. of 21th Scandinavian Symposium on Physical Acoustics, Ustaoset, Norway, edited by H. Hobæk (Department of Physics, University of Bergen, February 1998), pp. 51-52. 6 R.J. Astley, G.J. Macaulay, J.-P. Coyette, and L. Cremers, ``Three-dimensional wave-envelope elements of variable order for acoustic radiation and scattering. Part I. Formulation in the frequency domain,'' J. Acoust. Soc. Am. 103, 49-63 (1998). 7 L. Cremers, K.R. Fyfe, and J.P. Coyette, ``A variable order infinite acoustic wave envelope element,'' J. Sound Vib. 171, 483-508 (1994). 8 S. Kirkup, The Boundary Element Method in Acoustics (Swiftprint, Huddersfield, West-Yorkshire, England, 1998). 9 H.A. Schenck, ``Improved integral formulation for acoustic radiation problems,'' J. Acoust. Soc. Am. 44, 41-58 (1967). 10 S. Amini, P.J. Harris, and D.T. Wilton, Coupled Boundary and Finite Element Methods for the Solution of the Dynamic Fluid-Structure Interaction Problem (Springer-Verlag, Berlin, 1992). 11 S.M. Balabaev and N.F. Ivina, ``A mixed finite element-boundary element method in an analysis of piezoceramic transducers,'' Acoustical Physics 42, 149-154 (1996). 12 R. Bossut and J.-N. Decarpigny, ``Finite element modeling of radiating structures using dipolar damping elements,'' J. Acoust. Soc. Am. 86, 1234-1244 (1989). 13 J.T. Hunt, Knittel, and D. Barach, ``Finite element approach to acoustic radiation from elastic structures,'' J. Acoust. Soc. Am. 55, 269-280 (1974). 14 I. Harari, K. Grosh, T.J.R. Hughes, M. Malhotra, P.M. Pinsky, J.R. Stewart, and L.L. Thompson, ``Recent developments in finite element methods for structural acoustics,'' Arch. Comp. Meth. Eng. 3, 131-309 (1996). 15 D. Burnett, ``A three-dimensional acoustic infinite element based on prolate spheroidal multipole expansion,'' J. Acoust. Soc. Am. 96, 2798-2816 (1994). 16 P. Bettes, Infinite elements (Penshaw Press, Sunderland, U.K., 1992). 17 J.J. Shirron. ``Solution of exterior Helmholtz problems using finite and infinite elements,'' Ph.D. thesis, Department of Applied Mathematics, University of Maryland, 1995. 18 I. Harari and T.J.R. Hughes, ``A cost comparison of boundary element and finite element methods for problems of time-harmonic acoustics,'' Comp. Meth. Appl. Mech. Eng. 97, 77-102 (1992). 19 K. Gerdes, ``A summary of infinite element formulations for exterior Helmholtz problems,'' Comp. Meth. Appl. Mech. Eng. 164, 95-105 (1998). 20 L.E. Kinsler and A.R. Frey, Fundamentals of acoustics 2nd ed. (Wiley, New York, 1962). 21 Five piezoelectric ceramics, Bulletin 66011/F (Vernitron Ltd., England, 1976 [now Morgan Matroc Ltd.]).

Return to my homepage

About this document ...

Finite Element Modeling of Piezoceramic Disks
including Radiation into a Fluid Medium

This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)

Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html -split 0 -no_navigation abs2000.tex.

The translation was initiated by on 2000-03-09